ECUATII CU COEFICIENTI INTREGI
Daca consideram ecuatia ax + b = c, unde a, b, c ∈ Z si x ∈ M, cu M ⊂ Z.
Multimea M este multimea in care se rezolva ecuatia.
Rezolvarea ecuatiei se bazeaza pe urmatoarele proprietati:
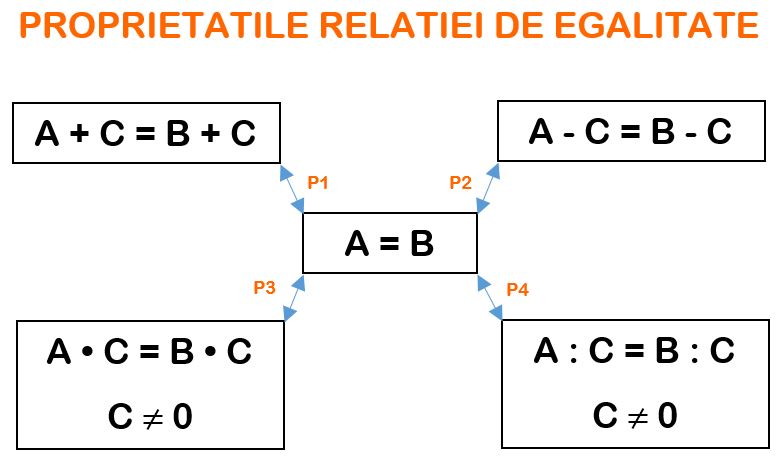
Exemplul 1:
5x + 6 = 11, x ∈ Z
5x + 6 - 6 = 11 - 6 (proprietatea P2 - scadem 6 din fiecare membru al egalitatii)
5x = 5
(5x) : 5 = 5 : 5 (proprietatea P4 - impartim fiecare membru al egalitatii la 5)
x = 1
1 ∈ Z, deci ecuatia are solutie unica 1.
Exemplul 2:
4x - 5 = -15, x ∈ Z
4x - 5 + 5 = -15 + 5 (proprietatea P1 - adaugam 5 la fiecare membru al egalitatii)
4x = -10
(4x) : 4 = (-10) : 4 (proprietatea P4 - impartim fiecare membru al egalitatii la 4)
x = (-10) : 4
Cum (-10) nu se poate imparti la 4 in Z, rezulta ca ecuatia nu are solutii.
