SISTEME DE AXE ORTOGONALE
Asa cum am precizat si in prima parte la capitolul numere intregi, o axa este o dreapta, pe care s-a considerat un punct fix numit origine si s-a ales o unitate de masura si un sens.
Asa cum am precizat si in prima parte la capitolul numere intregi, o axa este o dreapta, pe care s-a considerat un punct fix numit origine si s-a ales o unitate de masura si un sens.
Daca vom considera acum 2 drepte perpendiculare, cu aceeasi origine si aceeasi unitate de masura, putem spune ca am obtinut un sistem de axe ortogonale.
Acestea impart planul in 4 cadrane, iar fiecare punct din plan are acum 2 coordonate, o abscisa (coordonata de pe dreapta orizontala) si o ordonata (coordonata de pe dreapta verticala).
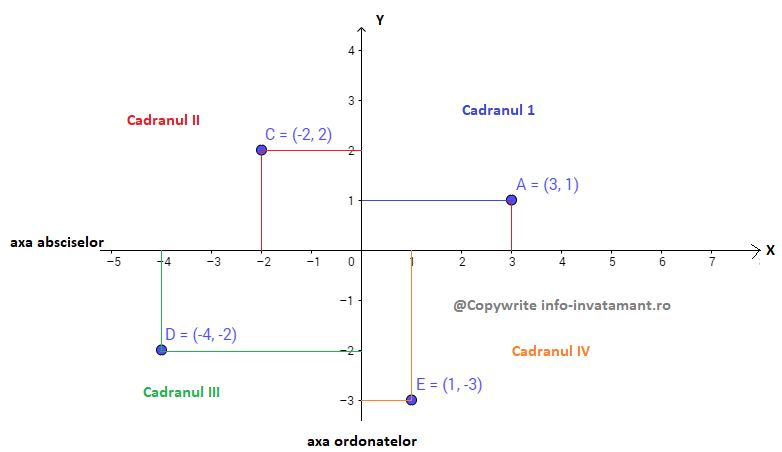
Punctul A din figura de mai sus, are coordonatele A(3;1), adica abscisa = 3 si ordonata = 1.
Pentru a reprezenta punctul A(3;1) in sistemul de axe ortogonale, incepem prin a trasa sistemul de axe xoy si a stabili unitatea de masura.
Apoi incepem cu abscisa si vom marca cu un semn unde abscisa are valoarea 3. Prin acel punct vom duce o linie perpendiculare pe axa absciselor.
Apoi, vom marca pe ordonata valoarea 1. Prin acel punct vom duce o linie paralela cu axa absciselor, pana cand vom intalni linia perpendiculara dusa anterior.
Punctul de intersectie al celor doua linii va fi punctul A(3; 1).
