Categorie

Puterea unui numar intreg. Calcule cu puteri

PUTEREA UNUI NUMAR INTREG. CALCULE CU PUTERI
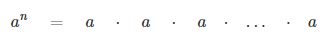
an = puterea n a numarului natural a
a = baza puterii
n = exponentul puterii
Ridicarea la putere este o operatie de ordinul al 3-lea. Acest lucru inseamna ca daca intr-un exercitiu nu exista paranteze, atunci se efectueaza mai intai ridicarile la putere, apoi inmultirile si impartirile, iar la sfarsit adunarile si scaderile.
 
REGULI DE CALCUL CU PUTERI

  1. Inmultirea puterilor care au aceeasi baza: 
  2. Impartirea puterilor care au aceeasi baza: 
  3. Puterea unui produs: 
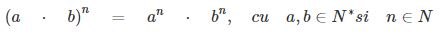
  4. Puterea unei puteri: 
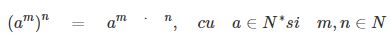
  5. Ridicarea unui cat la o putere: 
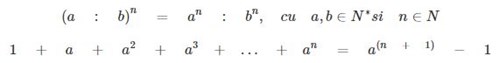
In cazul numerelor intregi, vom avea:

PATRAT PERFECT
Un numar obtinut prin ridicarea la puterea a 2-a a unui numar natural se numeste patrat perfect.
Pentru a arata ca un numar NU este patrat perfect, trebuie sa aratam ca este cuprins intre doua patrate de numere consecutive.
De exemplu: 115 nu este patrat perfect pentru ca 102 = 100 < 115 <121 = 112
Ultima cifra a unui patrat perfect poate fi numai 0, 1, 4, 5, 6 sau 9.
CUBUL UNUI NUMAR NATURAL
Un numar obtinut prin ridicarea la puterea a 3-a a unui numar natural se numeste cub perfect.
Pentru a arata ca un numar natural NU este cubul unui numar natural, trebuie sa aratati ca numarul respectiv este cuprins intre doua cuburi de numere naturale consecutive.
De exemplu: 115 nu este cub perfect pentru ca 43 = 64 < 115 < 125 = 53
COMPARAREA PUTERILOR
  1. Puteri cu aceeasi baza: Dintre doua puteri cu aceeasi baza, este mai mare cea care are exponentul mai mare. Cu alte cuvinte, daca bazele sunt egale se compara exponentii. Exemplu: 43 si 47. Bazele sunt egale (4), deci se compara exponentii: 3<7 => 43 < 47
  2. Puteri cu acelasi exponent: Dintre doua puteri cu acelasi exponent, este mai mare cea care are baza mai mare. Cu alte cuvinte, daca exponentii sunt egali, se compara bazele. Exemplu: 453 si 303. Exponentii sunt egali (3), deci comparam bazele: 45 > 30 => 453 > 303
  3. Puteri cu baze si exponenti diferiti: Pentru a compara doua puteri cu baze diferite si exponenti diferiti, se aduc puterile, daca este posibil, fie la aceeasi baza, fie la acelasi exponent.
Exemplu:
23 fata de 42
Atat bazele cat si exponentii sunt diferiti, insa observam ca bazele sunt puteri ale lui 2.
Prin urmare, 42 =(22)2 = 24
Acum putem compara 23 fata de 24, deci 23 < 24. Bazele sunt egale, 2, deci am comparat exponentii, iar 3<4.
Ce facem daca nu putem aduce la aceeasi baza?
In acest caz, se va afla c.m.m.d.c. al exponentilor.
Exemplu: 521 fata de 93 
Observam ca atat bazele cat si exponentii sunt diferiti si nu putem aduce la aceeasi baza.
Prin urmare, trebuie sa aflam c.m.m.d.c. al exponentilor.
21 = 3 * 7 ;   3 = 3 * 1
Rezulta ca c.m.m.d.c. = 3 (va readuc aminte ca la cel mai mare divizor comun se iau valorile comune, la puterea cea mai mica).
Vom scrie acum exponentii ca produs de c.m.m.d.c si inca ceva.
Deci : 521 = (57)3 = 781253 
In acest moment, observam ca avem acelasi exponent, deci putem compara bazele: 
521 = 781253 > 93

Categories: Matematica clasa a 6-a