CE ESTE ACELA UN DIVIZOR?
Un numar natural b este divizor al unui numar natural a, daca exista un numar natural c astfel incat a = b * c.
Altfel spus, daca un numar natural a se imparte exact la un numar natural b, atunci b este un divizor al lui a. Exemplu: 12 : 6 = 2, atunci putem spune ca 6 este un divizor al lui 12.
Se noteaza b | a si se citeste “b il divide pe a”.
Se mai poate nota si a ⋮ b si se citeste in acest caz “a se divide cu b” (e usor de tinut minte pentru ca seamana cu semnul de impartit).
Multimea divizorilor unui numar a este formata din toate numerele la care numarul a se imparte exact si se noteaza cu Da.
CE ESTE ACELA UN MULTIPLU?
Un numar natural a este multiplu al unui numar natural b, daca exista un numar natural c astfel incat a = b * c.
Altfel spus, daca un numar natural b se inmulteste cu orice numar natural, numerele obtinute se numesc multiplii ai numarului b. Exemplu: numarul b este 5, atunci numerele obtinute prin inmultirea lui 5 cu 1, 2, 3, 4, 5, 6…. ∞ sunt 5, 10, 15, 20, 25…∞, si formeaza multimea multiplilor numarului 5.
Multimea multiplilor unui numar a se noteaza cu Ma.
CRITERII DE DIVIZIBILITATE
- Divizibilitate cu 10: Un numar se divide cu 10, daca ultima cifra a numarului este 0. Exemplu: 50
- Divizibilitate cu 5: Un numar se divide cu 5, daca ultima cifra a numarului este 0 sau 5. Exemplu: 15, 60
- Divizibilitate cu 3: Un numar se divide cu 3, daca suma cifrelor numarului se imparte exact la 3. Exemplu: 27, pentru ca suma cifrelor numarului 27 este 2+7 = 9, iar 9:3 = 3.
- Divizibilitate cu 9: Un numar se divide cu 9, daca suma cifrelor numarului se imparte exact la 9. Exemplu: 279, pentru ca suma cifrelor numarului 279 este 2+7+9 = 18, iar 18:9 = 2.
- Divizibilitate cu 2: Un numar se divide cu 2, daca ultima cifra a numarului este un numar par, adica 0, 2, 4, 6 sau 8.
NOTIUNI
- Numar prim: numarul prim este acela care nu are ca divizori decat pe 1 si pe el insusi. In acest caza 1 si numarul insusi se numesc divizori proprii.
- Sirul numerelor prime este infinit !
- Doua numere naturale se numesc prime intre ele daca c.m.m.d.c.=1
- Numar compus: numarul compus este acela care pe langa 1 si el insusi, mai are cel putin 1 divizor. Divizorii diferiti de 1 si de numarul insusi se numesc divizori improprii.
- 1 nu este nici numar prim, nici numar compus !
CUM SE DESCOMPUNE IN FACTORI PRIMI UN NUMAR?
Pentru a descompune un numar in factori primi, trebuie sa gasiti, prin incercari succesive, pornind de la cel mai mic numar prim, toate numerele la care se imparte numarul dat, pana ramaneti cu 1.
De exemplu:
524:2 = 262
262:2 = 131
131 nu se imparte la 2, asa ca verificam cu urmatorul numar prim, adica 3.
Daca s-ar imparti la 3, ar trebui sa aiba suma numerelor un numar divizibil cu 3. Suma numerelor pentru 131 este 1+3+1=5, iar 5 nu se imparte la 3, deci prin urmare numarul 131 nu se imparte la 3.
Luam atunci urmatorul numar prim, adica 5. Ca sa se imparta la 5, ar trebui ca ultima cifra a numarului 131 sa fie 0 sau 5. In cazul nostru ultima cifra este 1, deci numarul 131 nu se imparte nici la 5.
Continuam cu urmatorul numar prim si tot asa…incercam numerele prime mai mici decat 131, iar daca nici unul dintre ele nu este un divizor al lui 131, atunci inseamna ca 131:131 = 1.
Prin urmare, numarul initial, 524, il putem scrie ca produs de factori primi astfel: 524 = 2 * 2 * 131 sau 524 = 22 * 131 * 1
Pentru a folosi conventia de scriere, in momentul cand vrem sa descompunem in factori primi, vom scrie astfel:
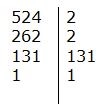
PROPRIETATI ALE RELATIEI DE DIVIZIBILITATE IN ℕ
- Orice numar natural a este divizibil cu el insusi : a|a, unde a∈N, a≠0
- Orice numar natural a este divizibil cu 1: 1|a, pentru a∈N
- Numarul 0 este divizibil cu orice numar natural a: a|0, pentru a∈N
- Daca numarul natural a este divizibil cu b, atunci orice multiplu al lui a va fi divizibil cu b. Explicatie: b | a, atunci a = b * c. Multiplul lui a, d = a * k, adica d = b * c * k, adica b | d.
- Daca a si b sunt divizibile cu c, atunci a+b si a-b sunt de asemenea divizibile cu c. Explicatie: a ⁞ c, rezulta ca a = c * x; b ⁞ c, rezulta b = c * y. In acest caz, putem scrie ca a + b = c * x + c * y = c * (x + y), notam x+y=d si rezulta ca a + b = c * d, deci c este un divizor al lui (a+b). Similar se explica si scaderea, a – b = c * x – c * y = c * (x – y). Notam x – y = m, rezulta a – b = c * m, deci c este un divizor al lui (a-b).
- Daca a | b si b | c atunci si a | c. Explicatie: a | b inseamna ca b = a * x. Daca b | c inseamna ca c= b * y = (a * x) * y = a * (x * y), adica a | c.
- Daca a | 1 inseamna ca a=1
- Daca a|b±c si a|b, atunci a|c. Explicatie: Daca a | b c, atunci b c = a * m; daca a | b atunci b = a * n, rezulta ca b + c = a * n + c = a * m, rezulta ca c = a * m – a * n, adica c = a * (m – n), deci a | c.
- Daca a | b atunci si a | nb
- Daca a | b, atunci si na | nb
- Daca a | b si c | d atunci ac | bd. Explicatie: a | b inseamna ca b = a * x; daca c | d inseamna ca d = c * y, deci b * d = (a * x) * (c * y) = (a * c) * (x * y), deci ac | bd.
CUM PUTEM AFLA CEL MAI MARE DIVIZOR COMUN?
Sunt mai multe metode pentru aflarea c.m.m.d.c, insa cea mai comuna si cea mai rapida poate, este descompunerea numerelor in factori primi si apoi se face produsul factorilor comuni, luati la puterea cea mai mica.
C.M.M.D.C = cel mai mare divizor comun
c.m.m.d.c = cel mai mare divizor comun = cel mai mare numar natural care divide numerele date.
Se noteaza d = (m, n).
Exemplu: avem numerel 125 si 45.
125 = 53 , iar 45 = 32 * 5
Factorul comun pentru cele 2 numere este 5, iar cea mai mica putere a lui 5 din cele 2 numere este 1, deci c.m.m.d.c = 5, d(125, 45) = 5.
CUM PUTEM AFLA CEL MAI MIC MULTIPLU COMUN?
Sunt mai multe metode pentru aflarea c.m.m.m.c, insa cea mai comuna si cea mai rapida poate, este descompunerea numerelor in factori primi si apoi se face produsul factorilor comuni si necomuni, luati la puterea cea mai mare.
C.M.M.M.C = cel mai mic multiplu comun
c.m.m.m.c = cel mai mic multiplu comun = cel mai mic numar natural nenul care se divide cu toate numerele date.
Se noteaza m = [a, b].
Exemplu: avem numerel 125 si 45.125 = 53 , iar 45 = 32 * 5
Deci c.m.m.m.c.= 53 * 32 = 1125
